Driving 8 WS2811 strips in parallel with an 8Mhz AVR

During a very short brainstorming session with Vinnie (where Vinnies part of the conversation consisted of mentioning that he had expected an 8-channel parallel version of the WS2811 driver) it became apparent that it should be possible to drive 8 WS2811 led strings in parallel from one AVR. This allows a single 8Mhz AVR to output at a speed of 266666 RGB LED values per second, or 10000 LEDs at a framerate of 25/s.

Doing this requires that the LED data is transposed in memory, i.e. that the first byte contains the first 8 bits of the channels, the second byte the second 8 bits, etc. If your application has the data in rgb-format in memory, some transposition is necessary. Transposition is fairly easy if you've got twice the memory: just create the transposed data by reading and shifting the source data. Doing the transposition in-place, without requiring twice the memory, is more difficult and boils down to in-place matrix transposition. There are many applications, however, for which it is fine to have the data pre-transposed in memory ("bitmap-like" applications can have their bitmaps pre-transposed).

We expect to use this technique in a number of POV applications.

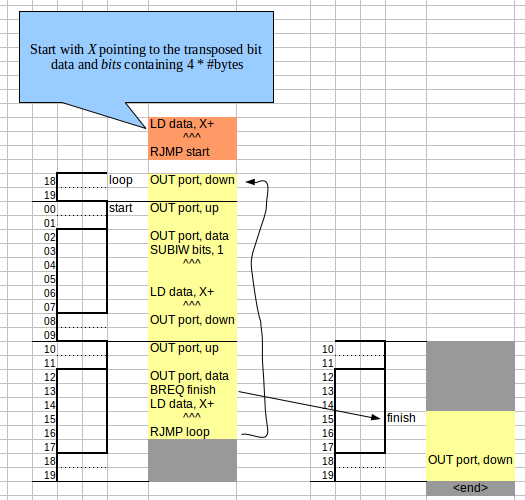
The code for transmission is below. This is definitely simpler than the single-channel version, but the single channel version had the advantage that the RGB (or rather GRB) values could stay in memory as such, without transposing. In this picture, as with the single-channel version, the NOP-instructions have been omitted for readability.

The code assumes one register filled with all ones (255), with alias 'up' and one register with all zeros, under the name 'down'.

Transposing bytes

Assume that the rgb-triplets for each channel are interleaved in memory. This means that the rgb values for the first LED that will be transmitted on pin 0 will be the first in the buffer, the rgb values for the first LED on pin 1 will be next etc. Transposing the RGB values can be done in two steps:

First gather all R, G and B values, i.e. for a buffer that is arranged as
```
RGBRGBRGBRGBRGBRGBRGBRGB
```
move all bytes so that the memory contains
```
RRRRRRRRGGGGGGGGBBBBBBBB
```
Then transpose each block of 8 bytes, so that the first byte will contain all most significant bits of all bytes ("bit 7"), the second byte contains all bit-6 values, etc.

The first step, gathering the R, G and B values boils down to transposing a 8X3 matrix and is solved by "following the cycles". The cycles for an 8X3 matrix can be pre-calculated and ignoring the cycles of size 1, consist of the following two cycles (zero-based indexing):

8, 18, 6, 2, 16, 13, 12, 4, 9, 3, 1
17, 21, 7, 10, 11, 19, 14, 20, 22, 15, 5

The code that can perform this transpose looks like this: <source lang=cpp>

include <stdint.h>

using value_type = uint8_t; using matrix = value_type[24];

inline void swap( uint8_t &left, uint8_t &right) {

   uint8_t buffer{left};
   left = right;
   right = buffer;

}

template< int index, int... indices> struct Rotator {

   static void rotate( matrix &m, value_type value)
   {
       swap( m[index], value);
       Rotator<indices...>::rotate( m, value);
   }

};

template< int index> struct Rotator<index> {

   static void rotate( matrix &m, value_type value)
   {
       m[index] = value;
   }

};

void transpose( matrix &m) {

   Rotator<8, 18, 6, 2, 16, 13, 12, 4, 9, 3, 1>::rotate( m, m[1]);
   Rotator<17, 21, 7, 10, 11, 19, 14, 20, 22, 15, 5>::rotate( m, m[5]);

}

</source>

This code compiles into a compact list of assembly instructions, essentially two instructions for each swap:

 b8:	90 85       	ldd	r25, Z+8	; 0x08
 ba:	81 81       	ldd	r24, Z+1	; 0x01
 bc:	80 87       	std	Z+8, r24	; 0x08

 be:	82 89       	ldd	r24, Z+18	; 0x12
 c0:	92 8b       	std	Z+18, r25	; 0x12

 c2:	96 81       	ldd	r25, Z+6	; 0x06
 c4:	86 83       	std	Z+6, r24	; 0x06

 c6:	82 81       	ldd	r24, Z+2	; 0x02
 c8:	92 83       	std	Z+2, r25	; 0x02

 ca:	90 89       	ldd	r25, Z+16	; 0x10
 cc:	80 8b       	std	Z+16, r24	; 0x10

 ce:	85 85       	ldd	r24, Z+13	; 0x0d
 d0:	95 87       	std	Z+13, r25	; 0x0d

 d2:	94 85       	ldd	r25, Z+12	; 0x0c
 d4:	84 87       	std	Z+12, r24	; 0x0c

 d6:	84 81       	ldd	r24, Z+4	; 0x04
 d8:	94 83       	std	Z+4, r25	; 0x04

etc, etc.

</source>

Driving 8 WS2811 strips in parallel with an 8Mhz AVR

From Just in Time

Transposing bytes